The latest incarnation of the Intel Xeon Phi product line, codename Knights Landing (KNL), is becoming more broadly available. As such, there is a lot of interest in how it performs, particularly when compared to other contenders in the high performance computing landscape. I have posted STREAM benchmark results for KNL earlier in my blog, which outlined the potential benefit of the high bandwidth memory (MCDRAM) of KNL. Let us have a look at a more complicated operation, which is neither limited by raw compute power nor by raw memory bandwidth: sparse matrix-matrix multiplication (aka. sparse matrix-matrix products).
Importance of Sparse Matrix-Matrix Multiplication
Multigrid methods are the methods of choice for many engineering problems. For the family of algebraic multigrid methods, there is no longer a notion of a physical 'grid'. Therefore, the scheme can be applied in a black-box manner for general systems. There is no guarantee that it will work, though!
[Skip this paragraph if you feel uneasy with the math]
The construction of multiple 'grids' during the setup stage of algebraic multigrid methods is purely algebraic and based on heuristics. The operator action on coarser grids is defined recursively via restriction and prolongation operators 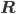 and
and 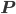 . The operator on the coarse grid
. The operator on the coarse grid 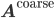 is then defined via
is then defined via
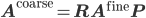
for a given fine grid operator
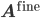 . All matrices on the right hand side are sparse; hence the computation of the coarse grid operator
. All matrices on the right hand side are sparse; hence the computation of the coarse grid operator 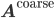 requires the computation of the triple matrix product
requires the computation of the triple matrix product 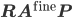 . The most common way to implement this triple product is to first compute
. The most common way to implement this triple product is to first compute 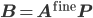 and then compute
and then compute 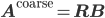 . There are other ways of computing the triple matrix product as well, but they are typically only a little faster, yet much more complicated. Thus, looking at standard sparse matrix-matrix multiplications provides a good idea about how fast the algebraic multigrid setup stage will run on a particular architecture.
. There are other ways of computing the triple matrix product as well, but they are typically only a little faster, yet much more complicated. Thus, looking at standard sparse matrix-matrix multiplications provides a good idea about how fast the algebraic multigrid setup stage will run on a particular architecture.
Sparse matrix-matrix multiplication has a very low arithmetic intensity: For each floating point operation, several integer comparisons and indirect loads are required. Moreover, the performance depends heavily on the sparsity pattern of the matrices. Thus, typical performances are on the order of 0.1 to 10 GFLOPs.
Benchmark Results
My benchmark code and result data for sparse matrix-matrix multiplication are available in a GitHub repository. Here I compare the performance obtained for squaring sparse matrices (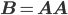 ) with the routine `mkl_dcsrmultcsr` from the multi-threaded Intel MKL library. The systems for comparison consume equal power: A dual-socket Xeon Haswell system, an older Xeon Phi Knights Corner PCI-Express board, and a recent Xeon Phi Knights Landing (with and without MCDRAM; self-hosted). The sparse matrices are the same as used in recent publications and are available in the Florida Sparse Matrix Collection.
) with the routine `mkl_dcsrmultcsr` from the multi-threaded Intel MKL library. The systems for comparison consume equal power: A dual-socket Xeon Haswell system, an older Xeon Phi Knights Corner PCI-Express board, and a recent Xeon Phi Knights Landing (with and without MCDRAM; self-hosted). The sparse matrices are the same as used in recent publications and are available in the Florida Sparse Matrix Collection.
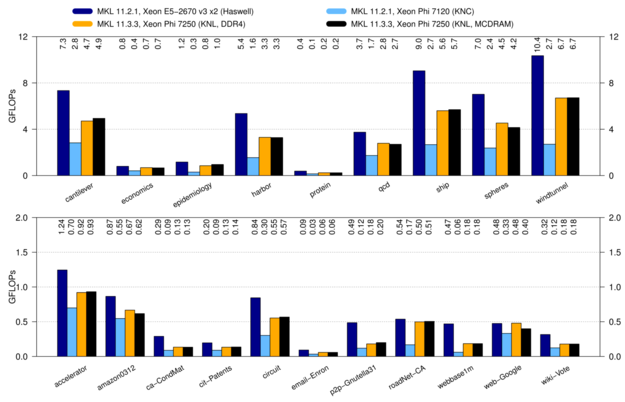
Benchmark results for sparse matrix-matrix multiplication on Intel Xeon and Xeon Phi. The matrices in the upper plot are somewhat more regular, whereas the sparse matrices in the bottom plot are very irregular.
The results show that a conventional Xeon system provides the best performance with 1.05 GFLOPs on (geometric) average. The Xeon Phi Knights Landing achieves 0.68 GFLOPs on average. Interestingly, it does not matter whether one uses MCDRAM or conventional DDR4 RAM. This suggests that the operation is not limited by memory bandwidth, and latency differences of MCDRAM and DDR4 play a minor role. The old Xeon Phi Knights Corner achieves only 0.23 GFLOPs. For comparison: On an NVIDIA Tesla K20m GPU one achieves an average performance of 0.20 GFLOPs with CUBLAS and 0.42 GFLOPs with ViennaCL.
Conclusion
Overall, a conventional dual-socket Xeon Haswell system provides about 50 percent better performance than Xeon Phi Knights Landing for sparse matrix-matrix multiplication. Thus, a Haswell Xeon system is the better choice for the setup stage of algebraic multigrid methods. Although I have not yet pinpointed the exact reason for the performance difference, I speculate that large L3 cache (30 MB) makes a big difference in favor of the Xeon system: Many rows in the right hand side factor are repeatedly accessed by different threads during the computation, so the Xeon CPU can serve many of those requests from L3 cache.
Considering that the setup stage and the solve stage of a good algebraic multigrid solver typically require about the same execution time, the Xeon Phi Knights Landing will have a hard time to outperform the Haswell Xeon system used for the comparison. If we keep in mind that newer Broadwell Xeons (and soon Skylake) offer higher memory bandwidth and even larger caches, it's unlikely that a Xeon Phi Knights Landing will provide any significant performance gains for algebraic multigrid methods.
Sparse matrix-vector multiplications, the second important operation when dealing with sparse systems, will be covered in a future blog post.
Resources
This blog post is for calendar week 19 of my weekly blogging series for 2016.